[기초통계] 정규분포

 

정규분포는 3시그마안에 확률의 99.7% 포함되어 있는 것으로 통계기법의 대부분은 정규분포를 따라야 한다는 조건이 있다! 때문에 따르지 않는다면 자료를 변환해야함

 

정규분포(Normal Distribution)

연속확률분포 중 하나

 

 

정규분포의 확률밀도함수

정규분포의 특징

평균=최빈값=중앙값

3시그마 안에 거의 포함됨(0.997)

* 그래서 정규분포표에 3.99까지밖에 없음

 

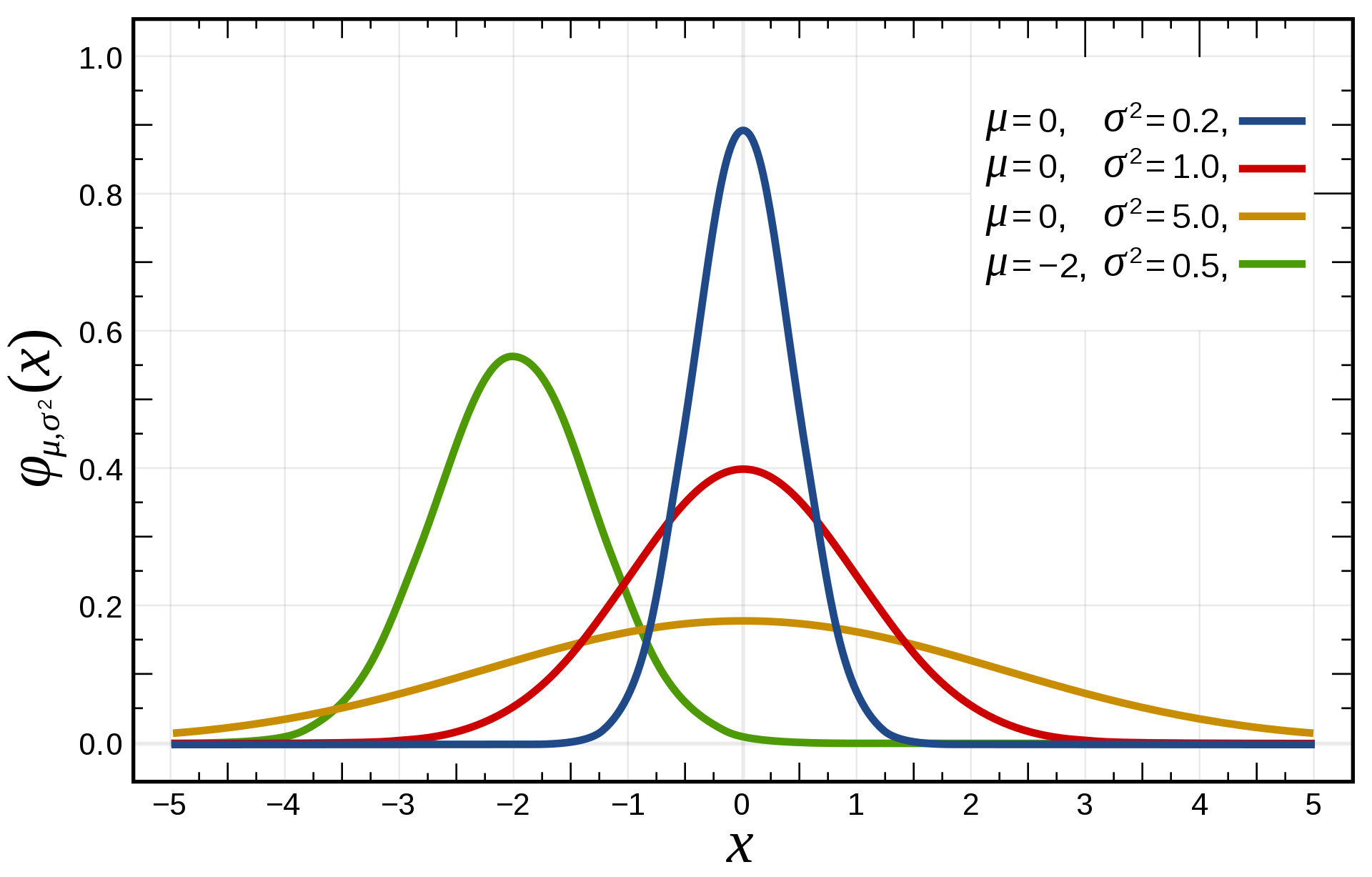
평균은 같고 분산이 다른, 분산은 같고 평균이 다른 정규분포의 확률밀도함수

분산은 같고 평균이 다를 경우 위치만 이동

평균은 같고 분산이 다를 경우 분포의 형태만 변화 = 분산이 커질수록 퍼짐~

 

 

표준정규분포(Standard normal distribution)

평균이 0이고 분산이 1인 정규분포

 

표준정규분포를 갖는 확률변수 = Z

Z는 0을 중심으로 대칭인 분포를 갖게 됨 = 표준정규분포는 0을 기준으로 0.5씩 총 1의 확률을 가짐

 

표준정규확률변수 

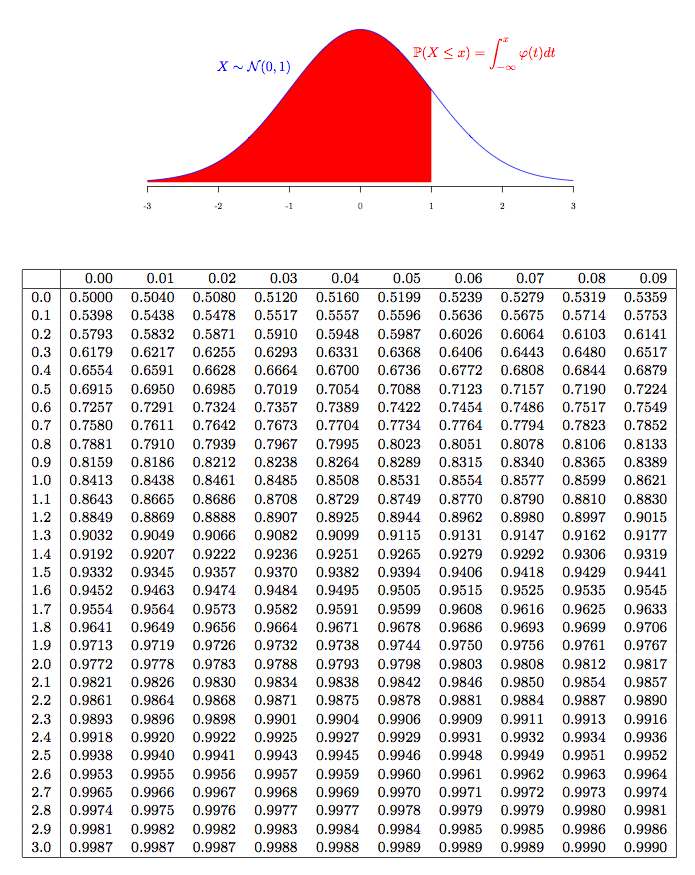
확률변수 X가 N(μ,σ²)일 때 표준화된 확률변수는

평균이 0이고 분산이 1인 정규분포 N(0,1)을 따름

 

 

예1) 중간고사 성적의 분포가 평균이 63, 분산이 100인 정규분포를 따를 때, 50점 이하의  학생은 몇퍼센트인지?

p[X<=50] = P[Z<=(50-63)/10] = P[Z=-1.3] = 0.0968 = 9.68%

 

예2) 위와 같은 분포일 때, 상위 10%의 학생에게 A를 주는 경우 몇 점 이상이 되어야 A를 받을 수 있는지?

P[X>=x] = 0.1

P[X>=1.28] = P[(X-63/10)>=1.28] = P[X>=75.8] = 75.8점 이상

http://imgur.com/NzMZfQR

 

이항분포의 정규분포근사

이항분포에서 n이 아주 크고 p가 0이나 1에 가깝지 않을 때 => np와 n(1-p)모두 클 때 정규분포에 가까워짐

n이 커짐에 따라 점점 정규분포 모양으로 바뀜을 볼 수 있음

 

확률변수 X가 이항분포, X~Bin(n,p)이고, np나 n(1-p)가 모두 클 경우(10이상)

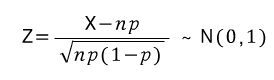
X는 근사적으로 평균이np, 표준편차가 √np(1-p)인 정규분포 N(0,1)을 따름

 

 

 

정규모집단의 가정을 조사하는 방법

모델이 정규분포를 따른다는 가정을 하고 있는데 정규모집단의 가정이 맞지 않는다면 의미없는 분석이 되기 때문에 추출한 표본의 분포가 정규분포를 따르는지 확인해야함

 

1. 그래프를 그려봐서 대칭성을 확인 - 히스토그램 등

2. 정규확률그림

 

정규확률그림

표본이이상적인 정규분포와 얼마나 비슷한지를 그림으로 보여줌

 

그리는 방법

1. 자료를 오름차순

2. 각 자료에 해당하는 점수를 계산

3. i번째 순서의 자료와 i번째 순서의 정규점수를 하나의 쌍으로 2차원 공간 상에 나타냄

정규점수 : N(0,1)에서의 이상적인 표본 = 표준정규분포의 확률밀도함수를 등확률 구간으로 나누어 주는 경계값(z)

 

해석법

그림이 직선인 경우 정규분포

그림이 곡선인 경우 정규분포 아님! 자료 변환 해야함

 

자료의 변환

표본의 크기가 작은 경우 통계분석을 하려면 모집단이 정규분포를 따른다는 가정이 필요함!

추출된 표본이 정규확률그림 등에서 정규분포와 상당히 벗어난 것으로 판단된 경우 자료를 변환하여 정규분포로 바꿔줌

큰 자료값을 더 크게 (오른쪽으로 편중된 경우) : x², x³

큰 자료값을 더 작게 (왼쪽으로 편중된 경우) : x¼, √x, logx, 1/x

 

 

 

 

참고자료

http://www.aistudy.co.kr/math/normal_lee.htm

https://ko.wikipedia.org/wiki/%EC%A0%95%EA%B7%9C_%EB%B6%84%ED%8F%AC